Scatter Diagram

(स्कैटर आरेख)

    सांख्यिकी (Statistics) में सहसंबंध (Correlation) का अर्थ दो चरों (Variables) के बीच संबंध की दिशा और मात्रा को समझना होता है। यह बताता है कि एक चर में परिवर्तन होने पर दूसरा चर किस प्रकार प्रभावित होता है।

    सहसंबंध के अध्ययन में स्कैटर आरेख (Scatter Diagram) एक अत्यंत सरल, दृश्यात्मक और प्रभावी विधि है, जिसके माध्यम से दो चरों के बीच संबंध को आसानी से समझा जा सकता है।

    स्कैटर आरेख को बिंदु आरेख भी कहा जाता है। इसमें दो चरों के मानों को ग्राफ पर बिंदुओं के रूप में दर्शाया जाता है। सामान्यतः स्वतंत्र चर (Independent Variable) को X-अक्ष पर और आश्रित चर (Dependent Variable) को Y-अक्ष पर अंकित किया जाता है।

    प्रत्येक युग्म (X, Y) को ग्राफ पर एक बिंदु (•) के रूप में प्रदर्शित किया जाता है। इन बिंदुओं के फैलाव और उनके झुकाव (Trend) से सहसंबंध की प्रकृति का अनुमान लगाया जाता है।

स्कैटर डायग्राम की परिभाषा

     स्कैटर डायग्राम वह आरेख है, जिसमें दो चरों से संबंधित आँकड़ों को ग्राफ पेपर पर बिंदुओं (Dots) के रूप में दर्शाया जाता है। एक चर को X-अक्ष (क्षैतिज अक्ष) पर तथा दूसरे चर को Y-अक्ष (ऊर्ध्वाधर अक्ष) पर रखा जाता है। दोनों चरों के मानों के युग्म (X, Y) को ग्राफ पर बिंदु के रूप में अंकित किया जाता है। इन बिंदुओं के फैलाव (Scatter) से यह ज्ञात होता है कि चरों के बीच किस प्रकार का सहसंबंध है।

स्कैटर डायग्राम की विशेषताएँ

    स्कैटर डायग्राम की कुछ प्रमुख विशेषताएँ निम्नलिखित हैं-

✍️ यह सहसंबंध को समझने की सबसे सरल और प्रारंभिक विधि है।

✍️ इसमें जटिल गणनाओं की आवश्यकता नहीं होती।

✍️ यह केवल सहसंबंध की दिशा और प्रकृति बताता है, उसकी सटीक मात्रा नहीं।

✍️ यह शोधकर्ताओं और विद्यार्थियों के लिए अत्यंत उपयोगी है।

✍️ यह सकारात्मक, नकारात्मक और शून्य सहसंबंध को स्पष्ट रूप से दर्शाता है।

स्कैटर डायग्राम बनाने की विधि

    स्कैटर डायग्राम बनाने की प्रक्रिया को निम्न चरणों में समझा जा सकता है-

(i) आँकड़ों का चयन:-

    सबसे पहले दो चरों से संबंधित आँकड़ों का चयन किया जाता है, जैसे- वर्षा और फसल उत्पादन, तापमान और आर्द्रता, जनसंख्या और संसाधन आदि।

(ii) अक्षों का निर्धारण:-

   एक चर को X-अक्ष पर और दूसरे चर को Y-अक्ष पर रखा जाता है। सामान्यतः स्वतंत्र चर (Independent Variable) को X-अक्ष पर और आश्रित चर (Dependent Variable) को Y-अक्ष पर रखा जाता है।

(iii) पैमाने का चयन:-

    दोनों अक्षों पर उपयुक्त पैमाना (Scale) निर्धारित किया जाता है, जिससे सभी मान ग्राफ पर सही ढंग से दर्शाया जा सकें।

(iv) बिंदुओं का अंकन:-

   प्रत्येक युग्म मान (X, Y) को ग्राफ पर केवल एक बिंदु के रूप में न कि रेखा रूप में अंकित किया जाता है।

(v) बिंदुओं का अवलोकन:-

   अंकित बिंदुओं के फैलाव को देखकर सहसंबंध की दिशा और प्रकार का अनुमान लगाया जाता है।

स्कैटर डायग्राम के प्रकार

     स्कैटर आरेख / डायग्राम में बिंदुओं वितरण की स्थिति के आधार पर सहसंबंध को निम्न प्रकारों में समझा जा सकता है-

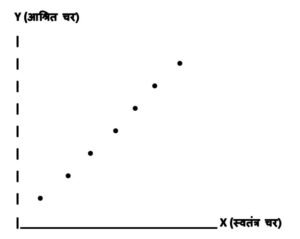
(i) सकारात्मक सहसंबंध (Positive Correlation)

    जब एक चर के बढ़ने पर दूसरा चर भी बढ़ता है, या एक चर के घटने पर दूसरा भी घटता है, तो उसे सकारात्मक सहसंबंध कहते हैं। स्कैटर डायग्राम में ऐसे बिंदु बाएँ से दाएँ ऊपर की ओर जाते हुए दिखाई देते हैं।

उदाहरण-

⇒ आय और उपभोग

⇒ वर्षा और कृषि उत्पादन

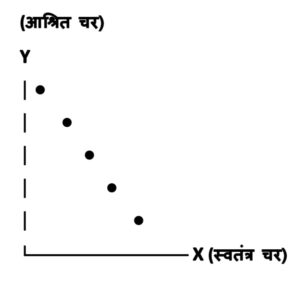
(ii) नकारात्मक सहसंबंध (Negative Correlation)

    जब एक चर के बढ़ने पर दूसरा चर घटता है, तो उसे नकारात्मक सहसंबंध कहते हैं। स्कैटर डायग्राम में बिंदु बाएँ से दाएँ नीचे की ओर ढलान बनाते हैं।

उदाहरण-

⇒ मूल्य और माँग

⇒ ऊँचाई और तापमान

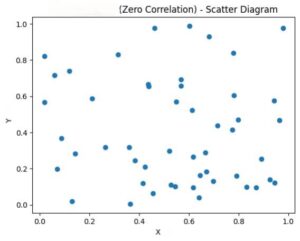
(iii) शून्य सहसंबंध (Zero Correlation)

    जब दो चरों के बीच कोई निश्चित संबंध नहीं होता, तो उसे शून्य सहसंबंध कहते हैं। स्कैटर डायग्राम में बिंदु अनियमित रूप से बिखरे होते हैं।
उदाहरण-

⇒ जूते का साइज और बुद्धि

⇒ जन्म-तिथि और परीक्षा-अंक

स्कैटर डायग्राम के लाभ

✍️ यह सहसंबंध को सरल और दृश्य रूप में प्रस्तुत करता है।

✍️ यह प्रारंभिक विश्लेषण के लिए अत्यंत उपयोगी है।

✍️ इसे बनाना और समझना आसान है।

✍️ यह आँकड़ों में किसी भी असामान्यता (Outlier) को स्पष्ट दिखा देता है।

✍️ यह आगे की सांख्यिकीय विधियों (जैसे Karl Pearson सहसंबंध) के लिए आधार प्रदान करता है।

सीमाएँ

    स्कैटर डायग्राम की निम्नलिखित सीमाएँ है-

✍️ यह सहसंबंध की सटीक मात्रा नहीं बताता।

✍️ बड़े आँकड़ों में बिंदु आपस में मिल जाते हैं, जिससे स्पष्टता कम हो जाती है।

✍️ यह केवल दो चरों के बीच संबंध दर्शा सकता है।

✍️ व्यक्तिगत व्याख्या (Subjective Interpretation) पर अधिक निर्भर करता है।

भूगोल एवं अन्य विषयों में उपयोग

   स्कैटर डायग्राम का प्रयोग भूगोल, अर्थशास्त्र, समाजशास्त्र, जनसंख्या अध्ययन, पर्यावरण अध्ययन आदि में व्यापक रूप से किया जाता है।

भूगोल में उपयोग जैसे-

  वर्षा और नदी प्रवाह, जनसंख्या घनत्व और संसाधन, तापमान और वनस्पति जैसे संबंधों को समझने के लिए स्कैटर डायग्राम अत्यंत उपयोगी है।

निष्कर्ष:

   अतः कहा जा सकता है कि सहसंबंध के अध्ययन में स्कैटर डायग्राम एक सरल, प्रभावी और उपयोगी ग्राफिकल विधि है। यह दो चरों के बीच संबंध की दिशा और प्रकृति को स्पष्ट रूप से दर्शाता है।

    यद्यपि इसकी कुछ सीमाएँ हैं, फिर भी प्रारंभिक विश्लेषण और शोध के लिए इसका महत्व अत्यधिक है। सांख्यिकी और भूगोल के विद्यार्थियों के लिए स्कैटर डायग्राम सहसंबंध को समझने का एक मजबूत आधार प्रदान करता है।